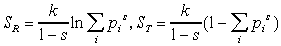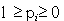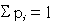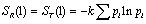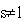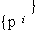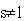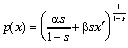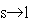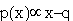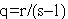Обобщенные меры информации и энтропии и их применение для вывода фрактальных статистических распределений
Башкиров А.Г.1, Витязев А.В.1, Рудой Ю.Г.2
1Институт динамики геосфер РАН, 117729, Москва, Ленинский
пр. 38 (корп.6), Россия
2Российский университет дружбы народов, 117198, Москва,
ул. Миклухо-Маклая 6, Россия
Дан краткий обзор применяемых в последние годы обобщенных мер информации
I и энтропии S = - I, введенных Реньи [1] и Цаллисом [2] в следующем виде
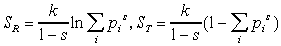 ,
,
где k - константа, s - любое положительное вещественное число, 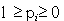 - вероятность дискретного i-го микросостояния, удовлетворяющего условию
нормировки
- вероятность дискретного i-го микросостояния, удовлетворяющего условию
нормировки 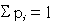 . В частном случае s=1 обе энтропии
совпадают с обычной энтропией Больцмана - Шеннона:
. В частном случае s=1 обе энтропии
совпадают с обычной энтропией Больцмана - Шеннона: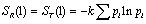 .
.
Введение величин SR (s) и ST (s) при 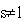 не противоречит
трем основным аксиомам Хинчина [3] для информационной меры любой системы,
описываемой вероятностным распределением
не противоречит
трем основным аксиомам Хинчина [3] для информационной меры любой системы,
описываемой вероятностным распределением 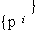 (или
его непрерывным обобщением p(x)). Случай
(или
его непрерывным обобщением p(x)). Случай 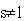 предполагает
альтернативную, но вполне естественную формулировку четвертой аксиомы,
определяющей меру информации для случая объединения двух подсистем в одну.
предполагает
альтернативную, но вполне естественную формулировку четвертой аксиомы,
определяющей меру информации для случая объединения двух подсистем в одну.
Наиболее существенным результатом введения информационных мер Реньи
и Цаллиса является возможность получения с их помощью не экспоненциальных
(гиббсовских или больцмановских), а распределений типа Вейбулла или степенных.
Действительно, применение принципа максимума информационной энтропии Джейнса
[4] к альтернативным энтропиям при учете дополнительного условия фиксированного
среднего значения какой-либо функции состояния системы, пропорциональной
xr, приводит к аналогу канонического распределения в виде
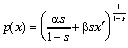 ,
,
где , - множители Лагранжа. В пределе 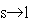 это
распределение переходит в каноническое распределение Гиббса, а для достаточно
больших x переходит в степенное распределение
это
распределение переходит в каноническое распределение Гиббса, а для достаточно
больших x переходит в степенное распределение 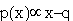 .
Показатель этого распределения
.
Показатель этого распределения 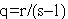 и, соответственно
значение числа Реньи или Цаллиса s определяются конкретными свойствами
рассматриваемой системы (см., например [5], где соответствующий расчет
выполнен для астрофизической задачи об импактном разрушении астероида).
и, соответственно
значение числа Реньи или Цаллиса s определяются конкретными свойствами
рассматриваемой системы (см., например [5], где соответствующий расчет
выполнен для астрофизической задачи об импактном разрушении астероида).
Распределения подобного рода могут представлять значительный интерес
в ряде задач биологии и экологии [6].
- A.Renyi. Probability theory. NHPC, Amsterdam, 1970.
- C.Tsallis. Journ.Stat.Phys. 52, 479 (1988).
- А.Я.Хинчин. Математические основания теории информации. Физматгиз,
1954.
- E.T.Jaynes. Phys.Rev. 106, 620 (1957), 108, 171 (1957).
- A.G.Bashkirov, A.V.Vityazev. Planetary and Space Sci. 44, 909-915 (1996).
- А.П.Левич. Структуры экологических сообществ. Изд-во МГУ, 1980.
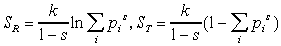 ,
,