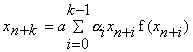Колебания и хаос в моделях динамики популяций лососевых рыб

Предлагается вариант общей модели динамики численности лососевых рыб, являющихся одним из основных объектов рыбного промысла на Дальнем Востоке. Базовая модель динамики численности популяции лососевых рыб имеет вид:

,

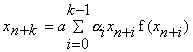
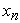
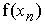
где - количество икры, отложенной всеми самками в n-м году, а - репродуктивный потенциал популяции, _i - доля рыб возраста (k-i) в нерестовом стаде, - коэффициент выживаемости на первом году жизни, k - максимальный возраст рассматриваемого вида рыб.

Модель была построена без учета внешних факторов (погодные условия, хищничество, конкуренция за пищу и т.д.), но ее исследование показало наличие последовательности бифуркаций, приводящих к возникновению замкнутых инвариантных множеств и удвоению периодов циклов. Таким образом, было установлено, что значительную роль играют внутрипопуляционные механизмы (плотностно-зависимая регуляция изменения численности, сложная возрастная структура).

Показано, что оптимальное управление популяцией вводит ее в такой режим, при котором исключена возможность каких бы то ни было колебаний численности, обусловленных внутрипопуляционными факторами. Это объясняется тем, что в стационарном случае при описанной стратегии промысла и оптимальной доле изъятия неподвижная точка остается устойчивой независимо от значения параметров системы.

С помощью этой модели предлагается способ решения задачи оптимального управления для произвольной популяции лососевых рыб на основе данных о численности нерестового стада и его возрастной структуре. При решении предполагалось, что промысел ведется таким образом, что из каждой возрастной группы изымается фиксированная одинаковая часть особей. Для этого уравнения были найдены и исследованы на устойчивость стационарные точки, а также разработана схема вычисления параметров, при которых в системе происходят бифуркации, вызванные потерей устойчивости неподвижной точкой.

Работа выполнена при финансовой поддержке РФФИ, грант № 96-01-00539.