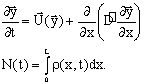Математическая модель структурообразования

В данной работе предпринята попытка построить компьютерную модель эмбриогенеза на основе экспериментальных данных. Рассматривается одномерная модель типа "реакция-диффузия", описывающаяся кинетическими уравнениями

(1)

-вектор переменных состояния (j=1..4), - вектор-функция реакций, - диагональная матрица коэффициентов диффузии, N(t)-число клеток, образовавшихся к моменту времени t.

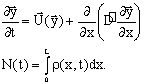
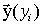
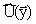
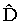
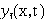
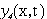
В предлагаемый вариант математической модели включены следующие переменные состояния и параметры: y₁(x,t) - плотность клеток; y₂(x,t) - концентрация субстрата; - концентрация ингибитора; - концентрация свободных радикалов; D₁₁= D₂₂=0; D₃₃, D₄₄ - коэффициенты диффузии ингибитора и свободных радикалов.

Первоначально рассматривается квазилинейная форма оператора реакций , а коэффициенты диффузии предполагаются постоянными. Элементы матрицы реакций _ij (i,j = 1..4) имеют следующие знаки:

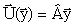
На границах отрезка [0, L] задаются краевые условия с нулевым потоком субстрата, ингибитора и свободных радикалов. Начальное распределение плотности клеток принимается равномерным .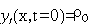

Для численного решения уравнений кинетики (1) выбрана симметричная неявная разностная схема с шеститочечным шаблоном [2]. Разрабатывается (в среде С++) программный комплекс с наращиваемой структурой и возможностью безболезненной модификации модулей, обрабатывающих вектор-функцию реакций. При кодировании используется объектно-ориентированный подход. Основная цель разработки - создание открытой вычислительной системы, допускающей возможно более широкий диапазон вариаций вида вектор-функции реакций. В настоящее время отлажены и тестируются отдельные модули программы. На следующем этапе предполагается рассмотреть задачу с нелинейной диффузией.

1. Мелехова О.П. О пространственно-временной программе эмбриогенеза. В настоящем сборнике.